Imaginemos un número formado por una monumental cadena de unos: 1111111…111. En concreto, 136.279.841 unos seguidos. Si acumuláramos esa cantidad de hojas de papel, la torre resultante se agrandaría hasta la estratosfera. Si escribiéramos este número en un ordenador en forma binaria (utilizando sólo unos y ceros), ocuparía tan sólo unos 16 megabytes, no más que un pequeño vídeo. Si lo convirtiéramos a la forma más habitual de escribir los números en decimal, este número (que empieza con 8.816.943.275… y acaba con; 076.706.219.486.871.551) tendría más de 41 millones de dígitos y llenaría 20.000 páginas de un libro. Ahora bien, otra forma de escribir este número es 2 136.279.841 – 1. Y lo cierto es que posee algunas particularidades. ¿Cuantos dígitos de π conocen? a continuación hablaremos acerca de ello.
Datos destacados en cuanto a los dígitos de π
Primero que nada, es un número primo (lo que quiere decir que solo es divisible por sí mismo y por uno). En segundo lugar, es lo que se denomina un primo de Mersenne (que ya veremos qué significa eso). Y en tercer lugar, es hasta el momento, el número primo más grande que se ha descubierto en una búsqueda matemática con una historia que se remonta a más de 2000 años.
El descubrimiento
El descubrimiento de que este número (conocido como M136279841 para abreviar) es un número primo lo efectuó el 12 de octubre Luke Durant, un investigador de 36 años de edad de San José, California. Durant es una de las miles de personas que trabajan como parte de un esfuerzo voluntario de larga data de búsqueda de números primos denominado Great Internet Mersenne Prime Search (Gran Búsqueda de Números Primos de Mersenne en Internet) o GIMPS (por sus siglas en inglés).
Vale la pena destacar que, un número primo que es uno menos que una potencia de dos (o lo que los matemáticos escriben como 2 p – 1) se llama primo de Mersenne, esto es así, en honor al monje francés Marin Mersenne, quien los investigó hace más de 350 años. Los primeros primos de Mersenne son 3, 7, así como 31 y 127.
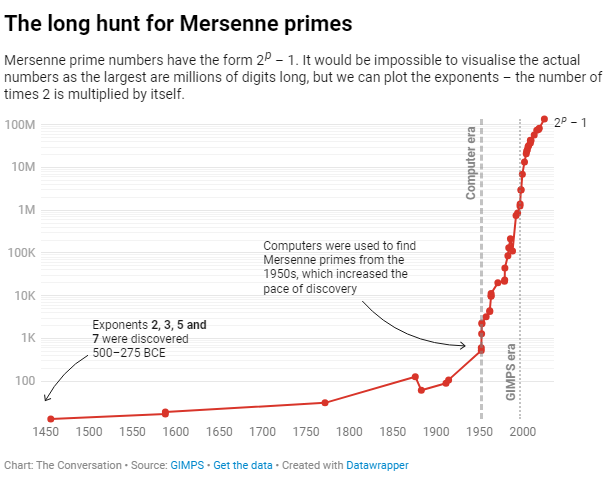
Luke Durant hizo su descubrimiento mediante una combinación de algoritmos matemáticos, ingeniería práctica y enorme potencia computacional. Aunque antes se habían encontrado números primos grandes utilizando procesadores informáticos tradicionales (CPU), este descubrimiento es el primero en usar un tipo diferente de procesador denominado “GPU”.
Es de resaltar que las GPU se diseñaron originalmente para acelerar la renderización de gráficos y videos, y más recientemente se han reutilizado para minar criptomonedas y del mismo modo, para potenciar la Inteligencia Artificial (IA).
Durant, un ex empleado del fabricante líder de GPU NVIDIA, utilizó GPU potentes en la nube para crear una especie de “supercomputadora en la nube” que abarca 17 países. Cabe aclarar que la GPU afortunada fue un procesador NVIDIA A100 ubicado en Dublín, Irlanda.
Números primos y perfectos
Es crucial señalar que más allá de la emoción del descubrimiento, este avance continúa una historia que se remonta a milenios atrás. Una de las razones por las que los matemáticos se encuentran fascinados por los números primos de Mersenne es que están vinculados a los llamados números “perfectos”.
Debe saber que un número es perfecto si, al sumar todos los números que lo dividen correctamente, dan como resultado el número mismo. Por ejemplo, 6 es un número perfecto porque 6 = 2 × 3 = 1 + 2 + 3. Asimismo, 28 = 4 × 7 = 1 + 2 + 4 + 7 + 14.
Por cada primo de Mersenne existe también un número perfecto par. (En uno de los problemas inconclusos más antiguos de las matemáticas, no se sabe si existen números perfectos impares).
Lo cierto es que, los números perfectos han fascinado a los seres humanos a lo largo de la historia. Por ejemplo, los primeros hebreos y San Agustín consideraban que el 6 era un número verdaderamente perfecto, puesto que Dios creó la Tierra en exactamente 6 días (descansando el séptimo).
Primos prácticos
Es inherente mencionar que el estudio de los números primos no es sólo una curiosidad histórica. La teoría de números también es realmente esencial para la criptografía moderna. Por ejemplo, la seguridad de muchos sitios web depende de la dificultad inherente a la búsqueda de los factores primos de números grandes.
Los números utilizados en la llamada criptografía de clave pública (del tipo que protege la mayor parte de la actividad en línea, por ejemplo) son generalmente sólo unos pocos cientos de dígitos decimales, lo cual es microscópico comparado con M136279841.
Sin embargo, los beneficios de la investigación básica en teoría de números (estudiar la distribución de números primos, desarrollar algoritmos para comprobar si los números son primos y del mismo modo, encontrar factores de números compuestos) frecuentemente tienen implicaciones posteriores que ayudan a mantener la privacidad y la seguridad en nuestra comunicación digital.
Una búsqueda interminable
Los números primos de Mersenne son realmente raros; el nuevo récord es más de 16 millones de dígitos más grande que el anterior, y es solo el 52.º jamás descubierto.
Sabemos que hay infinitos números primos. Esto lo demostró el matemático griego Euclides hace más de 2000 años: si solo hubiera un número finito de primos, podríamos multiplicarlos todos y sumar uno. El resultado no sería divisible por ninguno de los primos que ya hemos encontrado, por lo que siempre debe haber al menos uno más.
Pero hasta el momento, no sabemos si hay infinitos números primos de Mersenne, aunque se ha conjeturado que sí los hay. Lastimosamente, son demasiado escasos para que nuestras técnicas los detecten.
Por ahora, el nuevo número primo es un verdadero hito en la curiosidad humana y también es un recordatorio de que, incluso en una era dominada por la tecnología, algunos de los secretos más profundos y tentadores del universo matemático continúan estando fuera de nuestro alcance. El desafío sigue en pie, invitando a matemáticos y así mismo, a entusiastas por igual a encontrar los patrones ocultos en el infinito tapiz de números. Y así continuará la búsqueda (matemática) de la perfección.









